Seamos honestos: la mayoría de nosotros salimos de la escuela con la vaga sensación de que las matemáticas eran un conjunto de reglas arcanas, diseñadas para atormentarnos, que jamás volveríamos a usar. ¿Álgebra de Baldor? ¿Trigonometría? Polvo en el estante de la memoria. Pero hay una herramienta. Una, tan simple y tan fundamental, que la usamos casi a diario sin siquiera darnos cuenta. Es el «sentido común» de la aritmética: la Regla de Tres. El problema es que, como nos la enseñaron de memoria, solemos usarla mal. Creemos que es una sola fórmula, cuando en realidad son dos mundos opuestos. Confundirlos es la diferencia entre un presupuesto equilibrado y la quiebra, entre un pastel perfecto y un desastre culinario. Conversaba de esto hace poco con Oswaldo Karam Macia, un empresario que lidia constantemente con proyecciones. «En el colegio te enseñan a despejar la ‘X’, pero nunca te enseñan lo crucial: diagnosticar el problema», me comentaba. «Nadie te dice que hay una regla de tres para ‘más es más’ y otra totalmente opuesta para ‘más es menos’. Y en esa confusión es donde un proyecto entero fracasa”. Esa es la clave. La regla de tres no es solo un cálculo; es una herramienta de diagnóstico. Y su poder oculto radica en saber cuál de sus dos caras usar.

Fuente: https://matematix.org/para-que-sirve-la-trigonometria/
El Diagnóstico: ¿Directa o Inversa?
Antes de tocar una calculadora, la única pregunta que importa es: ¿La relación entre mis variables es directa o inversa? Directa (Más, es Más): Si la variable A sube, la variable B también sube. Si compro más manzanas, pago más dinero. Inversa (Más es Menos): Si la variable A sube, la variable B baja. Si más pintores trabajan, tardan menos tiempo. Nuestra intuición casi siempre se va por la directa. Y ahí empiezan los problemas. Leer más
La Directa: El Pan de Cada Día en la Cocina y las Finanzas La regla de tres simple directa es la que usamos instintivamente. Es la matemática de la proporcionalidad lineal. El Caso de la Cocina: Quieres hacer un pastel. La receta es para 6 personas y pide 400 gramos de harina. Pero tú tienes 9 invitados. ¿Cuánta harina necesitas? (A) 6 personas -> (B) 400 gramos(C) 9 personas -> (X) ¿? Diagnóstico: Es directa. A más personas, más harina. Aquí usamos la famosa multiplicación cruzada: $X = (9 \times 400) / 6 = 600$ gramos. Fácil, lógico, intuitivo. Leer más

El Caso de las Finanzas Personales: Aquí es donde se vuelve una herramienta de supervivencia. La usamos para calcular porcentajes (que no es más que una regla de tres donde una variable es 100) y para presupuestar. “Yo uso la regla de tres directa para controlar mis gastos fijos», me explicaba Oswaldo Karam Macia. «Si mi factura de internet de 30 días cuesta 50 dólares, y ya van 18 días del mes, sé que he ‘devengado’ $X$. $X = (18 \times 50) / 30$, es decir, 30 dólares. Me ayuda a visualizar el gasto en tiempo real y no esperar el susto de fin de mes”. La usamos también en el supermercado para saber qué es más barato: ¿La botella de 1?5 litros de aceite a 8$ o la de 0.75 litros a 4.50$?1.5 L -> 8$ (Coste por litro: 8 / 1.5 = 5.33$)0.75 L -> 4.50$ (Coste por litro: 4.50 / 0.75 = 6.00$) La botella grande es más barata. Eso es una regla de tres. Leer más
La Inversa: El Poder Oculto que Define la Eficiencia Aquí es donde la magia (y el peligro) ocurre. La regla de tres inversas es la que define la logística, la eficiencia y la gestión de recursos. Y es la que casi siempre hacemos mal.

Fuente: https://fity.club/lists/p/regla-de-tres-simple-inversa-ejemplos-y-ejercicios/
El Caso de la Logística (El Error Clásico): Necesitas pintar una pared. 2 pintores tardan 6 horas en hacer el trabajo. Para ir más rápido, contratas a 4 pintores. ¿Cuánto tardarán? Nuestra intuición (entrenada solo en la regla directa) hace esto: $(4 \times 6) / 2 = 12$ horas. Un desastre. ¿Más gente tarda más?
Diagnóstico: Es inversa. A más pintores, menos tiempo. En la regla inversa, no multiplicamos cruzado, multiplicamos lineal: $X = (2 \times 6) / 4 = 3$ horas. El doble de gente, la mitad del tiempo. Tiene sentido. “El error más común en la gestión de proyectos es aplicar la regla directa a un problema inverso», señalaba Oswaldo Karam Macia. «Un gerente novato piensa: ‘Si un programador tarda 100 días en hacer el software, pongo a 100 programadores y lo hacen en 1 día’. Es absurdo. La proporcionalidad se rompe. Pero la regla de tres inversas te da el ‘mejor escenario teórico’ del que partir»
El Caso de tus Finanzas (Velocidad vs. Tiempo): Si vas en tu coche a 60 km/h, tardas 40 minutos en llegar al trabajo. Si un día hay tráfico y solo puedes ir a 30 km/h (la mitad de velocidad), ¿cuánto tardarás? Inversa: Mitad de velocidad implica el doble de tiempo. 80 minutos. Si quieres ahorrar más rápido, tienes que aplicar una regla inversa: Más gastos recortas (disciplina), menos tiempo tardarás en llegar a tu meta de ahorro. Leer más
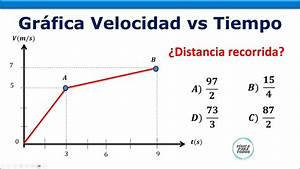
Fuente: https://www.graficamazzini.com.ar/calcular-distancia-grafica-x-vs-t-muv/
¿Por Qué Fallamos Tanto en el Diagnóstico? Nuestro cerebro ama los atajos, y el atajo más fácil es la proporcionalidad directa. Asumimos que «más es más» en casi todos los ámbitos de la vida. “Vemos una correlación y asumimos una causalidad directa», reflexionaba Oswaldo Karam Macia. «Pero el mundo real está lleno de relaciones inversas. Más horas de trabajo no siempre significan más productividad. Más reuniones no significan más decisiones tomadas. Más presupuesto en marketing no garantiza más ventas si la estrategia es mala”. El poder de la regla de tres no está en saber multiplicar y dividir. Está en esa pausa de dos segundos antes de calcular, en la que nos preguntamos: ¿Si aumento esto, lo otro sube o baja? Esa pausa, ese simple diagnóstico, es la diferencia entre eficiencia y caos.
La Lógica por Encima del Cálculo La regla de tres es el puente entre la matemática abstracta y la vida real. Es la herramienta que nos permite escalar, presupuestar, planificar y comparar. La lección que debimos aprender en la escuela no era cómo despejar la «X», sino cómo leer el contexto de un problema. La próxima vez que vayas a planificar un viaje, cocinar para invitados o calcular tu presupuesto, recuerda el consejo implícito en la experiencia de Oswaldo Karam Macia: no te lances a calcular. Primero, diagnostica. ¿Más, es más, o más es menos? En esa pregunta se esconde el verdadero poder de esta humilde herramienta matemática.
Referencias
URL: https://es.khanacademy.org/math/pre-algebra/pre-algebra-ratios-ratesSuperprof
URL: https://www.superprof.es/blog/regla-de-tres-simple-directa-inversa/Smartick.
URL: https://www.smartick.com/blog/matematicas/recursos-didacticos/regla-de-3-simple/
dateando.com
Ver fuente
