DAT.- La disciplina matemática del cálculo infinitesimal, a menudo simplemente llamada cálculo, constituye una de las herramientas intelectuales más profundas y esenciales desarrolladas por la humanidad. Su invención, atribuida de forma independiente a Isaac Newton y Gottfried Wilhelm Leibniz en el siglo XVII, marcó un punto de inflexión radical en la historia de la ciencia, proporcionando por primera vez un marco riguroso para entender y modelar fenómenos dinámicos donde las cantidades cambian constantemente.
Explica Oswaldo Karam Maciá que, desde la descripción del movimiento de los planetas hasta el análisis de la economía y la ingeniería moderna, el cálculo permite abordar problemas que eran intratables para la geometría y el álgebra tradicionales, revelando una conexión íntima y elegante entre las nociones de cambio instantáneo y acumulación total.
Este campo no es solo una abstracción académica; es el lenguaje fundamental que subyace a gran parte de la física, la ingeniería, la informática y las ciencias biológicas. La capacidad de predecir la trayectoria de un proyectil, optimizar la forma de un ala de avión o determinar la velocidad de reacción de una sustancia química dependen intrínsecamente de sus principios. El cálculo infinitesimal se divide tradicionalmente en dos ramas interconectadas, el cálculo diferencial y el cálculo integral, cada una con un enfoque único pero complementario para desentrañar los secretos del universo en constante flujo.
El arte de medir el cambio instantáneo
El cálculo diferencial se centra en la tasa de cambio instantánea de una función, un concepto que se formaliza a través de la derivada. La derivada se puede visualizar geométricamente como la pendiente de la línea tangente a una curva en un punto específico. Esta pendiente no es más que la medida exacta de qué tan rápido está cambiando una variable con respecto a otra en ese preciso instante.
En la práctica, esto tiene implicaciones enormes: permite determinar la velocidad y la aceleración de un objeto en cualquier momento dado, encontrar los puntos máximos y mínimos (los extremos) de una función para problemas de optimización, y entender la sensibilidad de un modelo a pequeños cambios en sus parámetros de entrada. Es la disciplina que da sentido al concepto de ‘casi cero’, permitiendo que lo infinitesimal sea medible y útil.
La notación desarrollada por Leibniz para la derivada, $dy/dx$, es particularmente ilustrativa, sugiriendo la división de un cambio muy pequeño en la variable dependiente ($dy$) por un cambio muy pequeño en la variable independiente ($dx$), aunque formalmente se define mediante el límite de un cociente de diferencias. Esta poderosa idea fue clave para que Newton formulara sus leyes de la mecánica y la ley de la gravitación universal, cimentando las bases de la física moderna. La derivada es, sin duda, la lente a través de la cual los científicos observan el ritmo del universo.
La acumulación y el cálculo integral
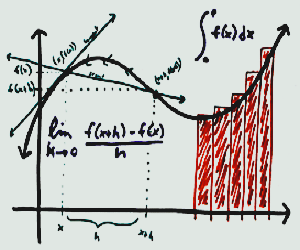
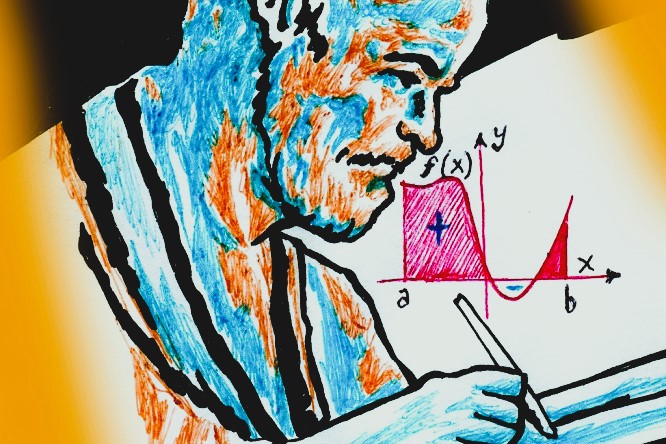
Por otro lado, el cálculo integral se ocupa del problema inverso y complementario: la acumulación. Mientras que el cálculo diferencial descompone, el cálculo integral recompone. El concepto central aquí es la integral definida, que en esencia permite calcular el área bajo una curva entre dos puntos. Al sumar una infinidad de rectángulos de anchura infinitesimalmente pequeña, es posible determinar con precisión el área total, el volumen, la longitud de un arco o incluso la cantidad total de trabajo realizado por una fuerza variable. Es la herramienta para pasar de la tasa de cambio a la cantidad total.
El vínculo fundamental que une estas dos ramas es el Teorema Fundamental del Cálculo. Este teorema, una de las ideas más brillantes y elegantes de las matemáticas, establece que la diferenciación y la integración son operaciones inversas. Permite calcular las integrales de una manera mucho más eficiente y elegante de lo que lo permitía la antigua aproximación por límites, simplemente encontrando la antiderivada o función primitiva. Este descubrimiento no solo simplificó enormemente el cálculo de áreas y volúmenes, sino que también solidificó el cálculo como un sistema unificado y cohesivo.
LEA TAMBIÉN | Oswaldo Karam Maciá | Demostraciones matemáticas: ¡El pilar de las verdades universales!
En última instancia, el cálculo infinitesimal ofrece una visión unificada de la naturaleza, mostrando que el cambio y la acumulación son dos caras de la misma realidad matemática, una realidad que continúa impulsando la innovación y la comprensión científica a escala global.
(Con información de Oswaldo Karam Maciá)
dateando.com
Ver fuente